[python] 백준 10830 :: 행렬 제곱 (분할 정복)
2023. 3. 11. 20:07ㆍAlgorithm
728x90
반응형
[행렬 제곱]
# 문제
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
# 입력
첫째 줄에 행렬의 크기 N과 B가 주어진다. (2 ≤ N ≤ 5, 1 ≤ B ≤ 100,000,000,000)
둘째 줄부터 N개의 줄에 행렬의 각 원소가 주어진다. 행렬의 각 원소는 1,000보다 작거나 같은 자연수 또는 0이다.
# 출력
첫째 줄부터 N개의 줄에 걸쳐 행렬 A를 B제곱한 결과를 출력한다.풀이
전체 코드
import sys
N, B = map(int, input().split())
A = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
# 행렬 곱셈 함수
def matrix_mul(arr1, arr2):
# 곱셈 결과를 저장할 2차원 리스트 생성
result = [[0] * N for _ in range(N)]
# 행렬 곱셈 연산 수행
for row in range(N):
for col in range(N):
s = sum(arr1[row][i] * arr2[i][col] for i in range(N))
result[row][col] = s % 1000
# 결과 반환
return result
# 분할 정복 함수
def power(n, arr):
# 종료 조건: n이 1일 때
if n == 1:
return arr
# n이 짝수일 때
if n % 2 == 0:
half = power(n//2, arr) # 절반을 계산
return matrix_mul(half, half) # 제곱 계산
# n이 홀수일 때
else:
return matrix_mul(arr, power(n-1, arr)) # n-1로 짝수로 만들어서 제곱 계산
# 결과 출력
for row in power(B, A):
print(*[r % 1000 for r in row])0. 풀이 방식
- 곱할 횟수를 반씩 나누어 가는 분할 정복 방식으로 접근한다.
- 곱해야 할 횟수가 홀수로 주어질 경우에는,
A^2 * A와 같은 경우가 생길 수 있어
단순히 행렬을 제곱하는 방식으로는 해결할 수 없다. - 따라서, 제곱이 아닌 행렬 두 개 arr1과 arr2를 곱한 결과를 리턴하는 함수를 만들어야 한다.
1. 행렬 곱셈 함수
행렬의 곱셈 구하는 방법
- 행렬을 곱하면 앞 행렬의 행 수와 뒤 행렬의 열 수로 이루어진 행렬이 만들어진다.
(이 문제에서는 어차피 같은 행렬을 곱하는 거니까 그대로 N * N 행렬이 나온다.) - 1행 1열에 들어갈 값은
앞 행렬의 1행의 요소들을뒤 행렬의 1열의 요소들과 하나씩 차례대로 곱한 값을 전부 더한다.
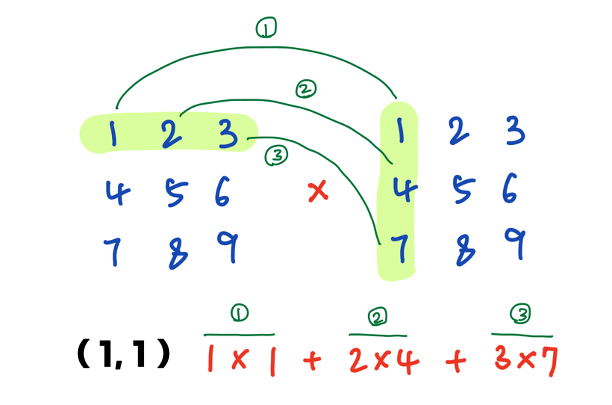
- 1행 2열에 들어갈 값은
앞 행렬의 1행의 요소들을뒤 행렬의 2열의 요소들과 하나씩 차례대로 곱한 값을 전부 더한다.

- 2행 1열과 2행 2열 계산
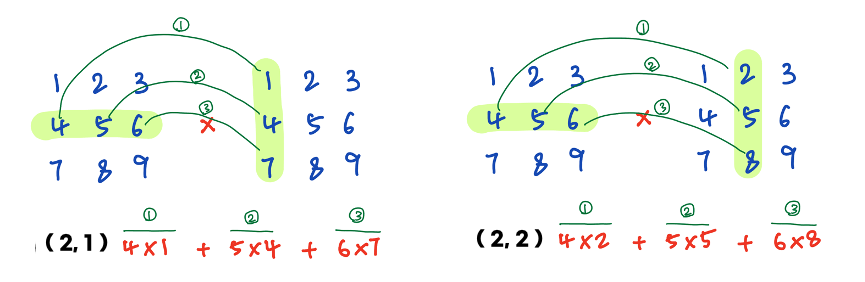
a행 b열의 값은
이렇게 앞의 행렬의a행의 요소를 하나씩, 뒤 행렬의b열의 요소를 하나씩
짝지어 곱한 값을 전부 더해주면 된다.- 이것을 코드로 나타내면 각 행/렬의 값은 아래처럼 구할 수 있다.
값 = 0 for i in range(N): 값 += 앞행렬[row][i] * 뒤행렬[i][col]- 이 값을 결과를 담을 리스트에 넣어주면 되는데,
문제에서 1000으로 나눈 나머지 값을 사용하라고 했으니 1000으로 나눈 나머지를 넣어준다.
그러면 행렬 곱셈 함수 완성!
# 행렬 곱셈 함수
def matrix_mul(arr1, arr2):
# 곱셈 결과를 저장할 2차원 리스트 생성
result = [[0] * N for _ in range(N)]
# 행렬 곱셈 연산 수행
for row in range(N):
for col in range(N):
s = sum(arr1[row][i] * arr2[i][col] for i in range(N))
result[row][col] = s % 1000
# 결과 반환
return result
2. 분할 정복 함수
종료 조건 설정
- n이 1이면 arr을 그대로 리턴한다.
# 종료 조건: n이 1일 때 if n == 1: return arr
n이 짝수일 경우
- n//2 값으로 분할 정복 함수를 다시 호출하고,
그 값으로 행렬의 곱셈을 한다.# n이 짝수일 때 if n % 2 == 0: half = power(n//2, arr) # 절반을 계산 return matrix_mul(half, half) # 제곱 계산
n이 홀수인 경우
- n이 3인 경우에는
arr * (arr * arr)
n이 5인 경우에는arr * (arr * arr) * (arr * arr)
이런식으로 arr에 짝수번 곱한 값을 곱해주면 되니까
arr과power(n-1, arr)를 실행한 값을 곱해준다.
# n이 홀수일 때
else:
return matrix_mul(arr, power(n-1, arr)) # n-1로 짝수로 만들어서 제곱 계산
3. 결과 출력
- 🚨 출력할 때도 값들을 1000으로 나눈 나머지를 출력해줘야 한다.
- 곱셈을 할 때 1000으로 나눈 값을 저장하기 때문에 이 과정이 필요 없을 것 같지만,,,
- 곱할 횟수가 1로 주어져서 곱셈을 수행하지 않아도
기존의 값이 1000보다 큰 경우에는 1000으로 나눈 나머지를 결과로 출력해야 정답으로 나온다ㅡㅡ..
# 결과 출력
for row in power(B, A):
print(*[r % 1000 for r in row])728x90
반응형
'Algorithm' 카테고리의 다른 글
| [python] 백준 2812 :: 크게 만들기 (스택) (0) | 2023.03.12 |
|---|---|
| [python] 백준 1629 :: 곱셈 (분할 정복, 모듈러 연산, 메모이제이션) (0) | 2023.03.11 |
| [python] 백준 2630 :: 색종이 만들기 (분할 정복) (0) | 2023.03.10 |