2023. 3. 27. 22:53ㆍAlgorithm
[행렬 곱셈 순서]
# 문제
크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.
예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에 행렬의 곱 ABC를 구하는 경우를 생각해보자.
AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.
BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.
같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.
행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 입력으로 주어진 행렬의 순서를 바꾸면 안 된다.
# 입력
첫째 줄에 행렬의 개수 N(1 ≤ N ≤ 500)이 주어진다.
둘째 줄부터 N개 줄에는 행렬의 크기 r과 c가 주어진다. (1 ≤ r, c ≤ 500)
항상 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.
# 출력
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같다.
풀이 방법
우선 이 문제를 풀기 위해서는 행렬을 곱했을 때 연산 횟수를 구해야 한다.
1. 두 행렬의 곱 연산 횟수 구하기
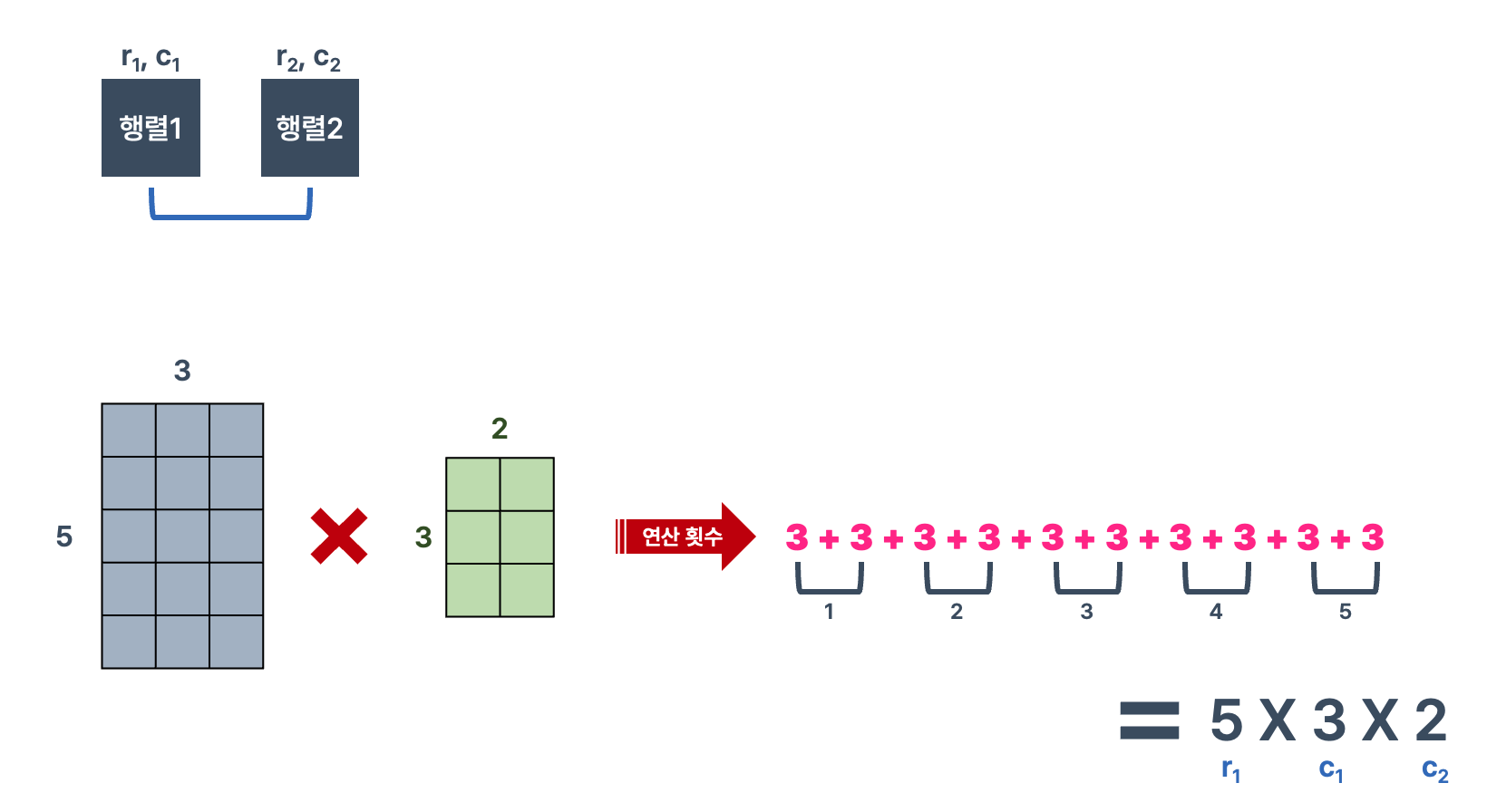
행렬 1과 행렬 2의 곱셈을 해보자!
크기가 5 X 3인 행렬 1과 크기가 3 X 2인 행렬 2를 곱할 때,
연산 횟수는 3을 두번씩 더한 것을 5번 반복하게 된다.
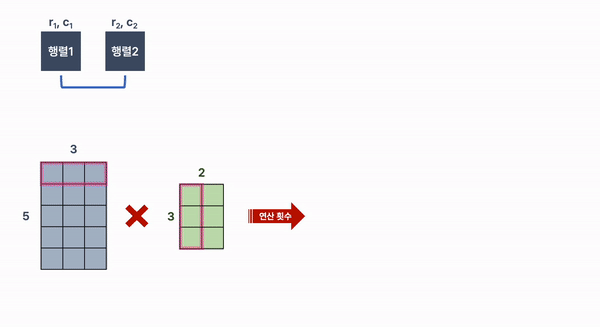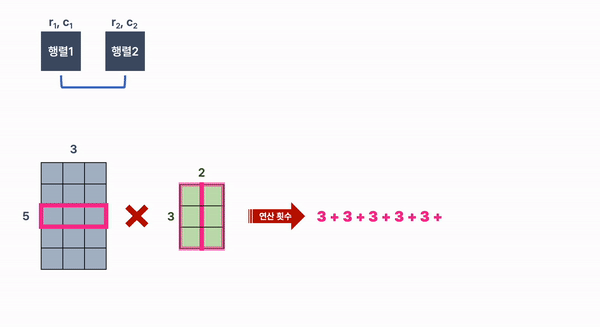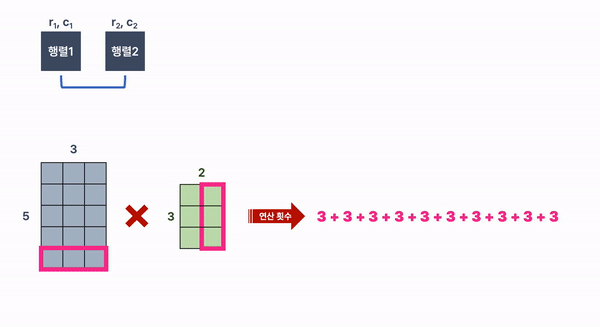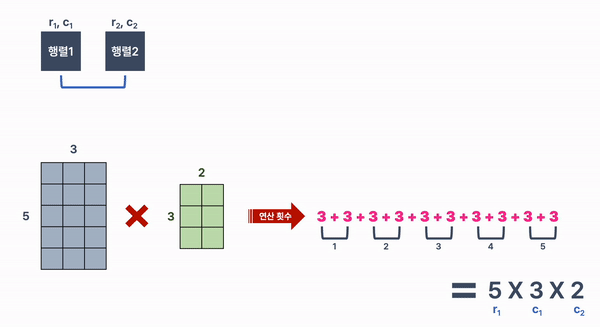
이것을 계산식으로 나타내면,행렬 1의 행 X 행렬 1의 열 X 행렬 2의 열 이 된다.
이번에는 행렬이 4개일 때 연산 횟수를 구해보자!
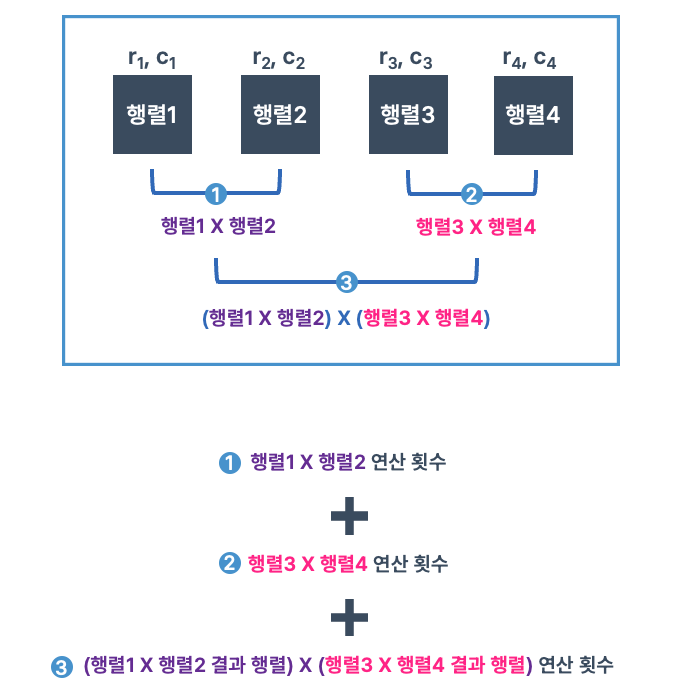
2. 세 개 이상인 행렬의 곱 연산 횟수 구하기
(행렬 1 X 행렬 2) X (행렬 3 X 행렬 4) 순서로 곱한다고 했을 때 연산 횟수를 구해보자!
- 위에서 두 행렬의 곱 연산 횟수를 구했던 것을 그대로 활용해서
1, 2) 묶여있는 행렬끼리의 곱 연산 횟수와 결과를 먼저 구하고,
3) 각 결과끼리 곱했을 때의 연산 횟수까지 구해서 전부 더해주면 된다.
3. 연산 경우의 수 확인하기
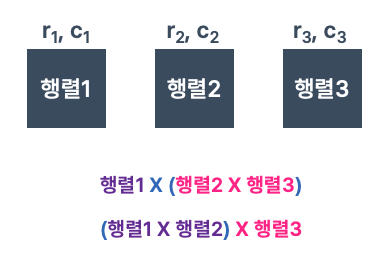
범위가 행렬 1 ~ 행렬 3인 경우
행렬이 1부터 3까지 있을 때는 아래와 같이 두가지 경우가 있다.
이 두가지 경우를 전부 계산했을 때 더 작은 값이 최소 연산 횟수가 된다.
범위가 행렬 1 ~ 행렬 4인 경우
행렬이 1부터 4까지 있을 때는 세가지 경우가 있다.

마찬가지로 각 경우의 연산 횟수를 계산했을 때, 그 중에서 가장 작은 값이 최소 연산 횟수가 된다.
🚨 작은 범위 먼저 계산해야 한다.
이렇게 행렬이 4개인 경우에는, 행렬 3개를 곱했을 때의 최소 연산횟수를 알아야
4개일 때의 연산 횟수를 구할 수 있는 것을 알 수 있다.
(마찬가지로 행렬이 3개인 경우에는 행렬 2개를 곱했을 때의 최소 연산횟수를 알아야 계산이 가능하다.)
따라서
현재 구해야하는 범위 안에서 생길 수 있는 더 작은 범위에 해당하는 연산을 먼저 해야 한다.
(구한 최소 연산횟수를 dp 테이블에 저장해두고 필요할 때 가져와서 활용한다.)
이제 이 내용을 활용해서 코드로 구현해봅시다~!
구현
1. dp 테이블 준비!
- 연산 횟수가 가장 최소가 되는 값을 저장하는 dp 테이블을 활용한다.
dp = [[0]*(N) for _ in range(N)]
👉 저장할 값
dp[시작행렬][끝행렬] = 최소 연산 횟수
👉 예시
문제에서 주어진 예시 (A의 크기가 5×3, B의 크기가 3×2, C의 크기가 2×6)
(AB)C의 연산 횟수는 5×3×2 + 5×2×6 = 30 + 60 = 90번
A(BC)의 연산 횟수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이므로
dp[A][C] = 90이 된다.
2. 간격이 작은 범위부터 계산한다.
위에서 연산 경우의 수를 확인하면서 살펴봤듯이
행렬 4개를 곱한 연산 횟수를 알기 위해서는 👉 3개를 곱한 연산 횟수를 알아야 하고,
3개를 곱한 연산 횟수를 구하기 위해서는 👉 2개를 곱한 연산 횟수를 알고 있어야 한다.
따라서, 간격이 작은 범위부터 연산 횟수를 계산해 나갈 것이다. (간격이 작은 것부터 계산한다.)
# 1. 간격이 1인 범위 먼저 전부 계산
행렬 1 ~ 2, 행렬 2 ~ 3, 행렬 3 ~ 4
# 2. 다음으로 간격이 2인 범위 전부 계산
행렬 1 ~ 3, 행렬 2 ~ 4
# 3. 마지막으로 간격이 3인 범위 계산
행렬 1 ~ 4
- 간격이 작은 것부터 하나씩 계산하기 위해서
term변수를 만들어서 '1'부터 '행렬의 개수 -1'까지 늘려가며 간격으로 활용할 것이다. - 적용해보면,
처음에는term이 1이므로 곱해야 하는 두 행렬은행렬 satrt와행렬 start+1이 된다.
(start가 1이면행렬 1과행렬 2의 연산횟수를 구하면 된다.)
for term in range(1, N):
for start in range(N): # 현재 범위의 첫행렬: start, 끝행렬: start + term
if start + term == N: # 범위를 벗어나면 무시
break
3. 계산할 범위 안에서 묶이는 경우를 고려한다.
term이 1일 때는 행렬 start와 행렬 start+1을 곱한 연산 횟수를 바로 구하면 되지만,
term이 1보다 크면 괄호로 묶어서 연산 순서를 바꿀 수 있으므로 여러 가지 경우가 생긴다.
예를 들어, term이 3인 경우에는 행렬 4개의 곱을 계산해야 하는데,
(시작 행렬: start, 끝 행렬: start+3 👉 start, start+1, start+2, start+3)
괄호로 묶었을 때, 각 괄호 안에 들어있는 행렬의 개수가 1개부터 3개까지 될 수 있다.
👉 즉, 괄호 안의 행렬이 최소 1개에서 최대 term개가 된다.

괄호 묶음의 모든 경우를 계산하기 위해서start부터 start+term 직전까지 증가하는 t 변수를 활용한다.
이 t 변수를 활용해서
괄호로 묶이는 묶음을 기준으로 왼쪽 묶음과 오른쪽 묶음을 나눠 보자.
왼쪽 묶음에 들어가는 행렬의 개수는 최소 1개부터 최대 term개까지 하나씩 늘어난다.
1) 왼쪽 묶음의 연산 횟수
dp[start][t] # 시작 행렬 : start, 끝 행렬: t- 왼쪽 묶음의 시작 행렬은
start로 고정된다.
(왼쪽 묶음의 시작 행렬은 항상 동일) - 왼쪽 묶음의 끝은
t가 된다.
(t는start부터 1씩 증가하므로 왼쪽 묶음의 끝은start,start+1,start+2,start+3, ...,계산 중인 범위의 마지막 행렬 - 1이 된다.)
2) 오른쪽 묶음의 연산 횟수
dp[t+1][start+term] # 시작 행렬: t+1, 끝 행렬: start + term- 왼쪽 행렬 묶음의 끝나는 부분이
t이므로, 오른쪽 묶음의 시작은t+1이 된다. - 오른쪽 묶음의 끝은 마지막에 해당하는
start+term이 된다.
(start로부터 term만큼의 간격을 갖는 행렬까지 계산하는 거니까!!!)
3) '왼쪽 묶음의 결과 행렬 X 오른쪽 묶음의 결과 행렬'의 연산 횟수
arr[start][0] * arr[t][1] * arr[start+term][1]- 두 묶음의 결과를 가지고 두 행렬의 곱셈 연산 횟수를 구할 때와 똑같이 하면 된다.
- 왼쪽 묶음의 결과
행L: 왼쪽 묶음 첫 행렬의 행 ==arr[start][0]열L: 왼쪽 묶음 끝 행렬의 열 ==arr[t][1] - 오른쪽 묶음의 결과
행R: 오른쪽 묶음 첫 행렬의 행 ==arr[t][1]열R: 오른쪽 묶음 끝 행렬의 열 ==arr[start+term][1] 행LX열LX열R
1~3을 더한 값이 최소가 되는 값을 dp[start][start+term]에 저장한다.
dp[start][start+term] = int(1e9) # 지금 계산할 첫행렬과 끝행렬
for t in range(start, start+term):
dp[start][start+term] = min(dp[start][start+term],
# 👇 1 + 2 + 3
dp[start][t]+dp[t+1][start+term] + arr[start][0] * arr[t][1] * arr[start+term][1])
끝!
- 시작 행렬부터 마지막 행렬의 최소 연산횟수를 출력한다.
print(dp[0][N-1]) # 시작 행렬 : 1, 끝 행렬: 행렬의 개수 -1
전체 코드
import sys
N = int(input())
arr = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
dp = [[0]*(N) for _ in range(N)]
for term in range(1, N):
for start in range(N): # 첫행렬 : i, 끝행렬: i+term
if start + term == N: # 범위를 벗어나면 무시
break
dp[start][start+term] = int(1e9) # 지금 계산할 첫행렬과 끝행렬
for t in range(start, start+term):
dp[start][start+term] = min(dp[start][start+term],
# 👇 1 + 2 + 3
dp[start][t]+dp[t+1][start+term] + arr[start][0] * arr[t][1] * arr[start+term][1])
print(dp[0][N-1])'Algorithm' 카테고리의 다른 글
| [python] 백준 2098 :: 외판원 순회 (DP, 비트마스킹) (0) | 2023.03.28 |
|---|---|
| [python] 백준 3055 :: 탈출 (BFS) (0) | 2023.03.21 |
| [python] 백준 2617 :: 구슬찾기 (DFS) (0) | 2023.03.21 |