[python] 백준 1197 :: 최소 스패닝 트리
2023. 3. 17. 04:31ㆍAlgorithm
728x90
반응형
[최소 스패닝 트리]
# 문제
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
# 입력
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.
# 출력
첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.
😱
우선,, 스패닝 트리가 무엇인지 먼저 아라보쟈!
Spanning Tree (신장 트리)
아래의 조건을 모두 만족하면 스패닝 트리이다.
- 모든 노드가 연결되어 있다.
- 사이클이 존재하지 않는다.
⭕️ 신장 트리의 옳은 예시
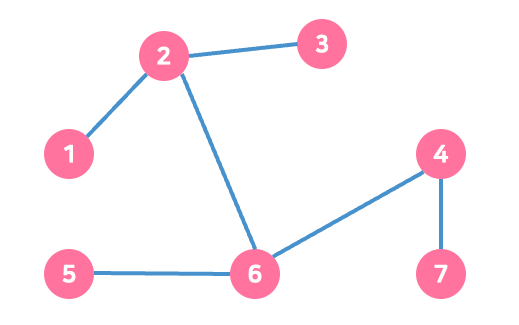
❌ 신장 트리가 아닌 예시
연결되지 않은 노드가 있거나, 사이클이 존재하는 경우 신장 트리가 아니다.
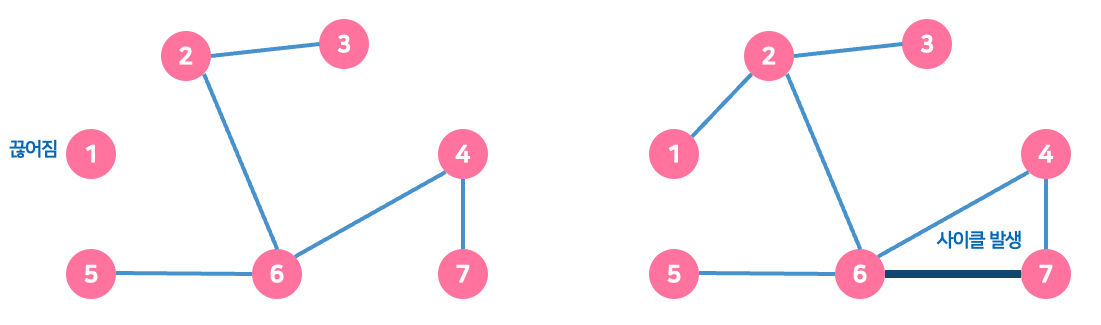
최소 신장 트리 구하기
- 최소 신장 트리 알고리즘: 신장 트리 중에서 최소 비용으로 만들 수 있는 신장트리를 찾는 알고리즘이다.
최소한의 비용을 갖는 신장 트리를 찾는 알고리즘, 크루스칼 알고리즘을 알아보자!
Kruskal Algorithm
- 크루스칼 알고리즘은 대표적인 최소 신장 트리 알고리즘이다.
1) 모든 간선을 비용 오름차순으로 정렬한다.
2) 비용이 적은 간선을 가져온다.
3) 이 간선이 연결되면 사이클을 발생시키는지 확인한다.
4) 사이클을 발생시키지 않는다면, 이 간선을 신장 트리에 포함시킨다.
~반복~이렇게 하면 항상 최적의 해를 보장할 수 있다.
1. 모든 간선을 비용 오름차순으로 정렬한다.
edges = [] # 간선
for _ in range(E):
a, b, cost = map(int, sys.stdin.readline().split())
edges.append((cost, a, b))
edges.sort() # 비용순 오름차순 정렬
2. 비용이 적은 간선을 가져온다.
- 1단계에서 오름차순으로 정렬해뒀으니, 그냥 하나씩 꺼내오면 된다!
for edge in edges:
cost, a, b = edge # cost 오름차순으로 정렬되어 있음
3. 이 간선이 연결되면 사이클을 발생시키는지 확인한다.
이 간선이 연결되면 사이클을 발생시키는지 알아내는 방법은,
주어진 간선의 각 노드의 부모 노드를 파악하는 것이다.
(각 노드의 부모 노드를 알아내서, 두 부모 노드가 같으면 이 간선은 연결되었을 때 사이클을 발생시킨다!!!)
💡 왜지,, 사이클은 뭐지,,,
연결된 노드가 같은 노드끼리 이어버리면 빙글빙글 돌아서 서로 만나게 되겠지, 이것이 바로 사이클~!
부모 노드는 각 노드가 연결된 제일 작은 노드를 의미한다.
이 부모 노드가 동일한 노드끼리 이어버리면 사이클이 발생한다.
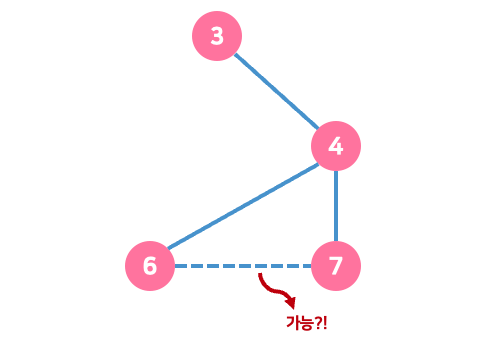
위 그림에서 점선으로 표시되어 있는 6-7을 잇는 간선을 이으면 사이클이 발생할까?!
- 7과 이어지는 제일 작은 노드는 3,
- 6과 이어지는 제일 작은 노드는 3
둘 다 3과 이어진다. 즉, 6-7 간선이 연결되면 사이클을 발생시킨다.🔥
이런 경우는 연결하면 안 된다.❌ 사이클이 발생하면 신장 트리가 아니니까~!
자 그럼 일단 부모 노드를 알아내야겟꾼
2-1) 부모 테이블을 만든다.
- 인덱스를 노드로, 값을 부모 노드로 넣을 것이다.
parent[노드] = 부모노드 - 노드는 1부터 주어지므로, 부모 테이블의 크기는 노드의 개수 + 1로 한다.
(인덱스 0은 안 쓸 거니까!) - 처음에는 일단 자기 자신으로 초기화한다.
(노드 1의 부모는 1, 노드 2의 부모는 2 ... )
# 부모를 담을 테이블 (parent[노드] = 부모노드)
parent = [0] * (V + 1)
# 부모를 자기 자신으로 초기화
for i in range(1, V+1):
parent[i] = i
2-2) 부모 노드가 같은지 검증한다.
2번의 for 문과 이어진다.
- 비용이 제일 적은 간선을 가져와서, 그 간선에 연결된 각 노드의 부모가 같은지 확인한다.
(부모가 같다는 것은 같은 집합에 속하는 것을 의미한다. 같은 집합에 속하는 것은 이으면 안된다.)
for edge in edges:
cost, a, b = edge # cost 오름차순으로 정렬되어 있음
if find_parent(a) != find_parent(b): # 같은 집합이 아니면,
- 아래는 부모를 찾는 함수이다.
함수를 재귀적으로 호출하면서 부모 테이블 값을 바로바로 갱신해주어 시간 복잡도를 개선했움 (경로 압축 기법)
# 부모 찾는 함수
def find_parent(x):
if parent[x] != x:
parent[x] = find_parent(parent[x])
return parent[x]
4. 사이클을 발생시키지 않는다면, 간선을 신장 트리에 포함시킨다.
2~3번의 for 문과 이어진다.
result = 0
for edge in edges:
cost, a, b = edge # cost 오름차순으로 정렬되어 있음
if find_parent(a) != find_parent(b): # 같은 집합이 아니면,
union_parent(a, b) # 연결
result += cost # 연결된 것 cost 누적- 비용을 저장할 변수
result를 새로 선언했다. - 간선을 이을 때마다 해당 간선의 비용을
result에 누적하고, 이 값을 최종 결과로 출력할 것이다. - 실제로 간선을 잇는 부분은
union_parent(a, b)👈🏻 이 함수 내부에서 이루어진다.
간선을 신장 트리에 포함시키는 함수
union_parent(a, b) 함수 안에서 뭘 하나 보자!
def union_parent(a, b):
# 집합(부모 노드) 찾기
a = find_parent(a)
b = find_parent(b)
# 큰 거에서 작은 거로 연결
if a < b:
parent[b] = a
else:
parent[a] = b👉🏻 연결할 두 노드의 부모를 찾아서 이어준다.
🤔 Why?

- 노드를 이을 때는 큰 노드에서 작은 노드 방향으로 이어야 하고, 작은 노드가 큰 노드의 부모가 된다.
즉, 노드를 이으려면 큰 노드의 부모를 작은 노드로 설정하기만 하면 된다!! - 🚨그런데,,,,
노드 3과 노드 2를 연결한다고 했을 때,
노드 2가 1과 연결되어 있으므로
노드 3의 부모 노드도 2가 아닌 1이 되어버린당 - 그러므로, 간선이 연결될 때마다 부모 노드를 갱신해줘야 한다!
3과 2를 연결할 때 3 -> 2로 끝나는 게 아니라, 3과 연결할 2의 부모를 찾아서 3 -> 1로 바꿔줘야 한다는 것이다!! - 부모 노드를 연결해주는 것이니, 우선 부모 노드를 찾는 함수
find_parent를 호출해서 찾고,
큰 부모 노드를 더 작은 부모 노드로 연결, 즉, 부모 노드끼리 연결되게 해준다.
자기자신과 부모는 당연히 연결되어 있으니, 부모 노드끼리만 이어주면 연결이 쭉- 이어진다. - 이렇게 하나씩 연결을 이어나가고, 연결되지 않은 것중에서 제일 적은 비용을 하나 둘 추가하다 보면 최소 신장 트리가 완성된다. 👏👏👏
끝!
전체 코드
import sys
V, E = map(int, input().split()) # 정점의 개수, 간선의 개수
# 부모를 담을 테이블 (parent[노드] = 부모노드)
parent = [0] * (V + 1)
# 부모를 자기 자신으로 초기화
for i in range(1, V+1):
parent[i] = i
# 부모 찾는 함수
def find_parent(x):
if parent[x] != x:
parent[x] = find_parent(parent[x])
return parent[x]
# 간선 연결하는 함수(집합 합치기)
def union_parent(a, b):
# 집합(부모 노드) 찾기
a = find_parent(a)
b = find_parent(b)
# 큰 거에서 작은 거로 연결
if a < b:
parent[b] = a
else:
parent[a] = b
edges = [] # 간선
for _ in range(E):
a, b, cost = map(int, sys.stdin.readline().split())
edges.append((cost, a, b))
edges.sort() # 비용순 오름차순 정렬
result = 0
for edge in edges:
cost, a, b = edge # cost 오름차순으로 정렬되어 있음
if find_parent(a) != find_parent(b): # 같은 집합이 아니면,
union_parent(a, b) # 연결
result += cost # 연결된 것 cost 누적
print(result)728x90
반응형
'Algorithm' 카테고리의 다른 글
| [python] 백준 1260 :: DFS와 BFS (0) | 2023.03.17 |
|---|---|
| [python] 백준 5639 :: 이진 검색 트리 (1) | 2023.03.17 |
| [python] 백준 5904 :: Moo 게임 (분할정복) (0) | 2023.03.16 |