[python] 백준 1707 :: 이분 그래프
2023. 3. 18. 21:39ㆍAlgorithm
728x90
반응형
[이분 그래프]
# 문제
그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.
그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.
# 입력
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호 u, v (u ≠ v)가 빈 칸을 사이에 두고 주어진다.
# 출력
K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.이분 그래프
집합이 두 개 있을 때, 인접한 노드끼리 서로 다른 집합에 넣을 수 있다면 이분 그래프이다.
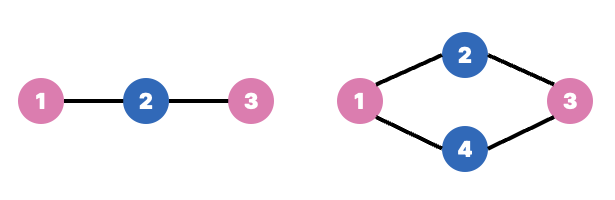
⭕️ 인접한 노드끼리 서로 다른 집합에 들어가게 만들 수 있으면 이분 그래프이다.
(같은 집합은 같은 색으로 표시했음)
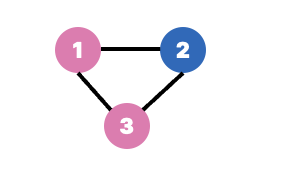
❌ 이렇게 인접한 노드끼리 어찌해도 다른 집합에 속하게 만들 수 없으면 이분 그래프가 아니다.
풀이
0. 풀이 방법
- DFS로 탐색을 하면서
인접 노드로 탐색을 이어나갈 때, 현재 집합과 다른 집합으로 표시해두고
인접 노드 중에서 현재 노드의 집합과 같은 집합에 속한 노드를 만나게 되면 NO를 반환하면 된다! - 그리고 이 문제에서는
그래프가 이어지지 않고 끊어져있는 경우가 있을 수 있기 때문에 모든 노드에서 DFS 탐색을 해야 한다.
1. 현재 노드의 집합과 인접한 노드의 집합을 저장한다.
- 방문 여부를 표시하는
visited리스트를 활용한다.0: 방문하지 않음1: 집합 A-1: 집합 B - 초기에 DFS의 인자
group에 1을 담아 DFS를 호출하고,
인접 노드로 타고 가면서 DFS를 호출할 때는-group을 전달해서
현재 노드와 인접 노드의 group을 다른 값으로 넣어준다.
현재 노드가 1이면
인접 노드는 -1이 되고
인접 노드의 인접 노드는 1이 들어가겠지!
계속 반전 반전 반전 ~!def DFS(start, visited, graph, group):
visited[start] = group # 현재 노드의 그룹 저장
# 인접 노드 탐색
for v in graph[start]:
if visited[v] == 0: # 아직 방문하지 않은 노드
DFS(v, visited, graph, -group) # -group : 현재 노드의 그룹과 다른 값 전달
2. 인접 노드끼리 다른 집합에 속하는지 확인한다.
- 이미 방문한 노드라면 (
visited[v] == 0이 아니면)
현재 노드의 group과 인접 노드의 group 값이 다른지 확인한다. - 현재 노드의 group과 인접 노드의 group이 다르면 아직까지는 이분그래프임!
- 현재 노드의 group과 인접 노드의 group이 똑같으면
인접 노드끼리 같은 집합에 들어있는 거니까 이분 그래프가 아니다!
이때 False를 리턴한다.
else:
if visited[v] == group: # 이미 방문한 곳 중에서 노드가 현재 그룹과 같으면 이분 그래프가 아님
return False
- 그룹이 겹쳐서 False를 리턴한 경우에는 탐색을 멈추고 호출된 함수들에서도 False를 리턴해야 하므로,
DFS를 재귀적으로 호출할 때 리턴값을 받아서 False인 경우에 리턴하도록 한다.
# 인접 노드 탐색
for v in graph[start]:
if visited[v] == 0: # 아직 방문하지 않은 노드
# -group : 현재 노드의 그룹과 다른 값 전달
result = DFS(v, visited, graph, -group)
if not result:
return False
else:
if visited[v] == group: # 이미 방문한 곳 중에서 노드가 현재 그룹과 같으면 이분 그래프가 아님
return False
return True
3. 모든 노드에 대해 DFS를 수행한다.
- 입력값을 받아서 방문하지 않은 모든 노드에 DFS를 호출한다.
- DFS가 False를 리턴하면 바로 멈추고 출력 ㄱㄱ
for _ in range(k):
V, E = map(int, sys.stdin.readline().split())
graph = [[] for _ in range(V+1)]
visited = [0] * (V+1)
for _ in range(E):
a, b = map(int, sys.stdin.readline().split())
graph[a].append(b)
graph[b].append(a)
for i in range(1, V+1):
if visited[i] == 0:
result = (DFS(i, visited, graph, 1))
if not result:
break
print("YES") if result else print("NO")
끝!
전체 코드
import sys
sys.setrecursionlimit(10**6)
k = int(input())
def DFS(start, visited, graph, group):
visited[start] = group # 현재 노드의 그룹 저장
# 인접 노드 탐색
for v in graph[start]:
if visited[v] == 0: # 아직 방문하지 않은 노드
# -group : 현재 노드의 그룹과 다른 값 전달
result = DFS(v, visited, graph, -group)
if not result:
return False
else:
if visited[v] == group: # 이미 방문한 곳 중에서 노드가 현재 그룹과 같으면 이분 그래프가 아님
return False
return True
for _ in range(k):
V, E = map(int, sys.stdin.readline().split())
graph = [[] for _ in range(V+1)]
visited = [0] * (V+1)
for _ in range(E):
a, b = map(int, sys.stdin.readline().split())
graph[a].append(b)
graph[b].append(a)
for i in range(1, V+1):
if visited[i] == 0:
result = (DFS(i, visited, graph, 1))
if not result:
break
print("YES") if result else print("NO")728x90
반응형
'Algorithm' 카테고리의 다른 글
| [python] 백준 21606 :: 아침 산책 (DFS) (0) | 2023.03.19 |
|---|---|
| [python] 백준 11724 :: 연결 요소의 개수 (0) | 2023.03.17 |
| [python] 백준 1260 :: DFS와 BFS (0) | 2023.03.17 |