[python] 백준 6549 :: 히스토그램에서 가장 큰 직사각형 (스택)
2023. 3. 14. 17:27ㆍAlgorithm
728x90
반응형
[히스토그램에서 가장 큰 직사각형]
# 문제
히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.
히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.
# 입력
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤ 1,000,000,000)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.
# 출력
각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.
💡 참고한 블로그 👉🏻 codable
0. 풀이 방법
- 각 그래프 막대의 길이를 확인하여 이전의 막대보다 긴 막대기가 나오면 stack에 push한다.
- 이전 막대보다 짧은 막대를 만나면
stack에 들어있는 막대들로 만들 수 있는 가장 큰 넓이를 구한다.
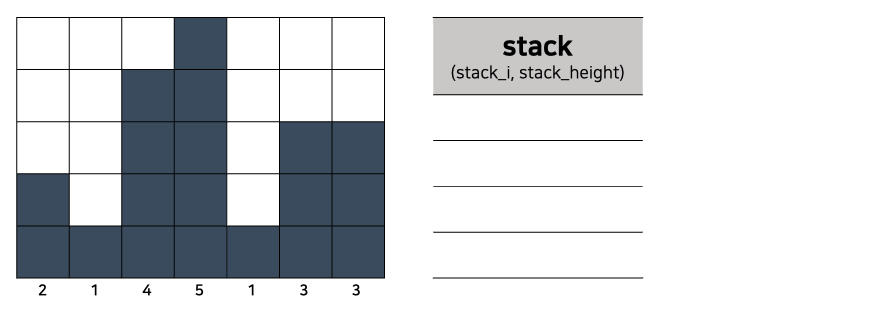
1. 스택이 비어있으면 스택에 현재 막대기를 추가한다.
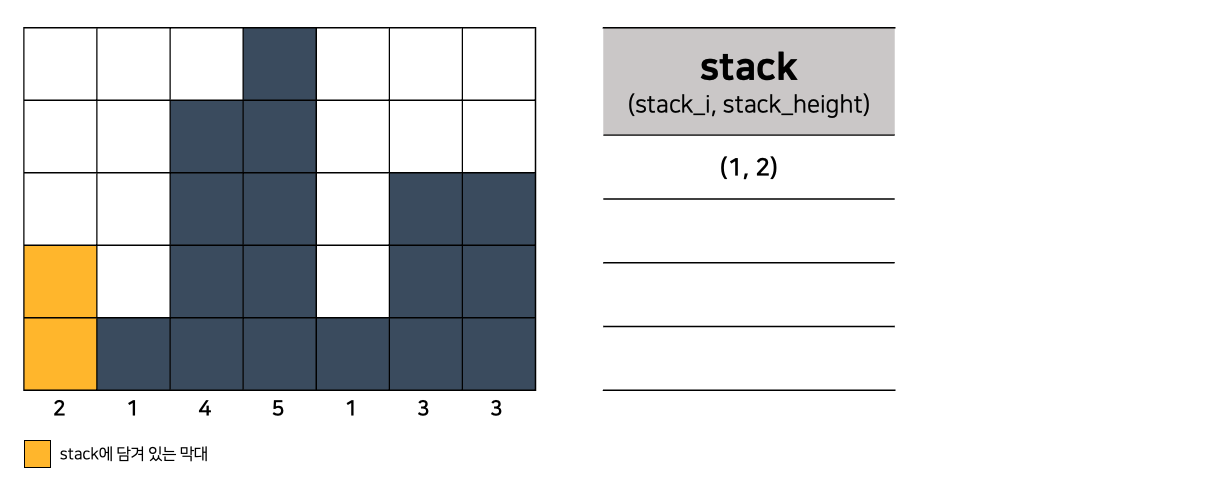
- stack이 비어있어서 첫번째 막대가 stack에 추가되었다.
if not stack:
stack.append((i, height)) # 스택에 현재 막대기를 추가합니다.
2. 스택에 마지막으로 들어간 막대 보다 짧은 막대를 만나면 스택에 들어있는 막대의 넓이를 계산한다.
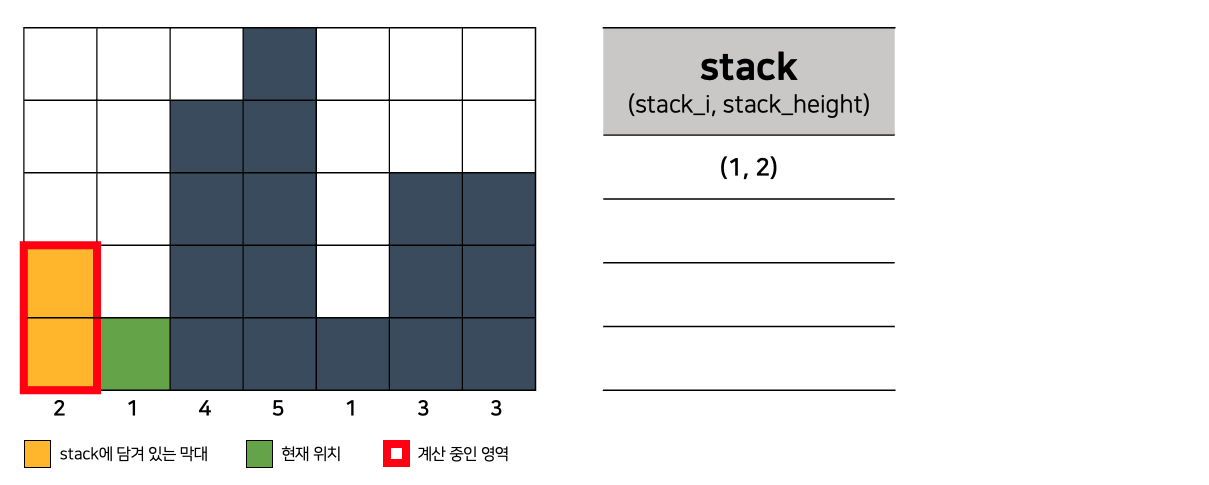
- 현재 위치는 초록색으로 표시된 인덱스 2에 위치해있다.
- 현재 위치의 막대기는 길이가 1로, 스택에 마지막으로 들어간 2보다 작다.
# 스택의 가장 위쪽 막대기보다 현재 막대기의 높이가 작으면
if stack and stack[-1][1] > height:
- 이 경우, 스택에 들어있는 막대로 만들 수 있는 넓이를 계산한다.
- 지금은 이걸 꺼내고 나면 스택에 남은 게 없으니, 시작인 1부터 현재 인덱스만큼을 width로 잡고 height를 곱해서 넓이를 구한다.
(i - width_start) * stack_height
(스택에 남은 값이 있는 경우는 아래에서 설명 ㅎㅎ😅)
while stack: # 스택에서 빼내며 최대 직사각형 넓이를 계산합니다.
stack_i, stack_height = stack.pop()
width_start = 1
result = (i - width_start) * stack_height
max_result = max(result, max_result)
3. 스택에 들어있는 막대를 꺼낼 때는, 현재 막대의 길이보다 큰 것까지만 꺼낸다.
- 🚨스택에 들어있는 막대 중에서 현재 막대의 길이보다 큰 것들만 꺼내서 계산해야 한다.
Why?
- 현재 막대 길이와 같거나 더 짧은 막대들은 이후 반복을 더 통과하면서 width를 더 길게 가져갈 수 있기 때문이다.
(width는 현재 index를 기준으로 하니까 반복을 오래 유지할수록 width가 길어짐!)
How?
- stack에는 막대기가 오름차순으로 들어가므로 (이전 값보다 큰 경우에만 push했으니까!)
stack에 남아있는 마지막 막대의 길이가 현재 반복의 height와 같거나 작으면 pop 하지 않게break를 걸어주면 된다. - stack이 비었을 때도 같이 break!
if not stack or stack[-1][1] <= height:
break
4. 스택에 마지막으로 들어간 막대 보다 긴 막대를 만나면 스택에 추가한다.
- 2번에서 막대를 꺼냈으므로(pop) 스택이 비게 되어 1단계에서 (2,1)이 들어간다.
(1단계 : 스택이 비어있으면 스택에 현재 막대기를 추가한다.) - 따라서, 현재 stack에는 (2,1)이 들어있는 상태다.
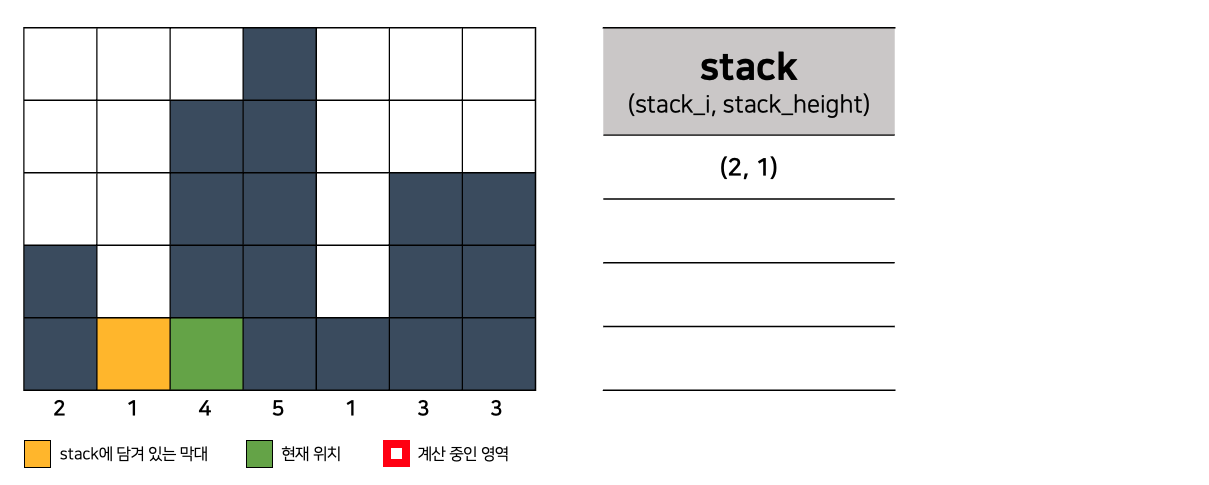
- 지금 만난 막대기가 stack에 담겨있는 막대보다 기니까 이거도 stack에 넣어준다.
# 스택이 비어 있거나 스택의 가장 위쪽 막대기보다 현재 막대기의 높이가 크거나 같으면
if not stack or stack[-1][1] <= height:
stack.append((i, height)) # 스택에 현재 막대기를 추가합니다.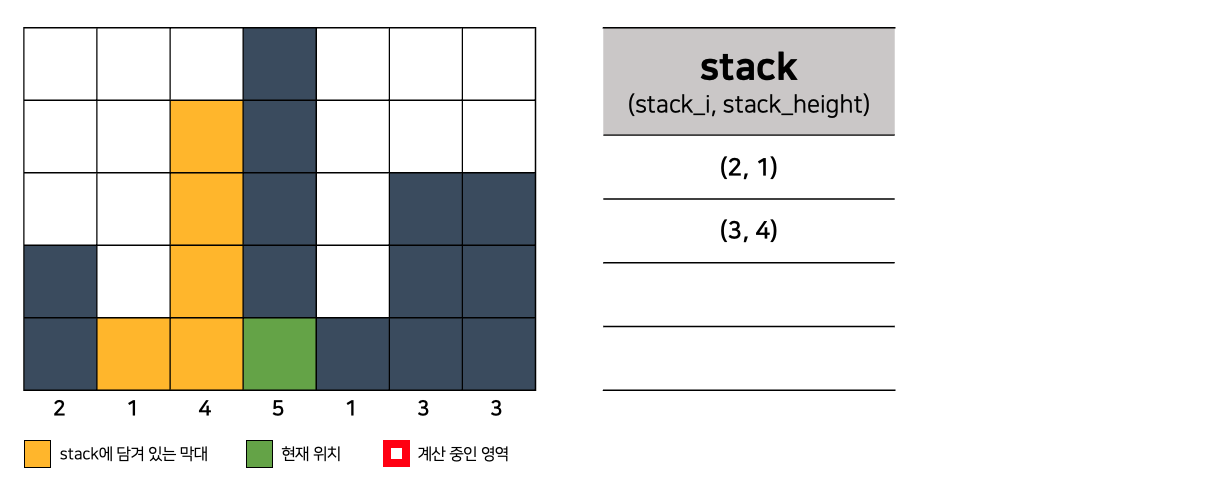
- 반복한다.
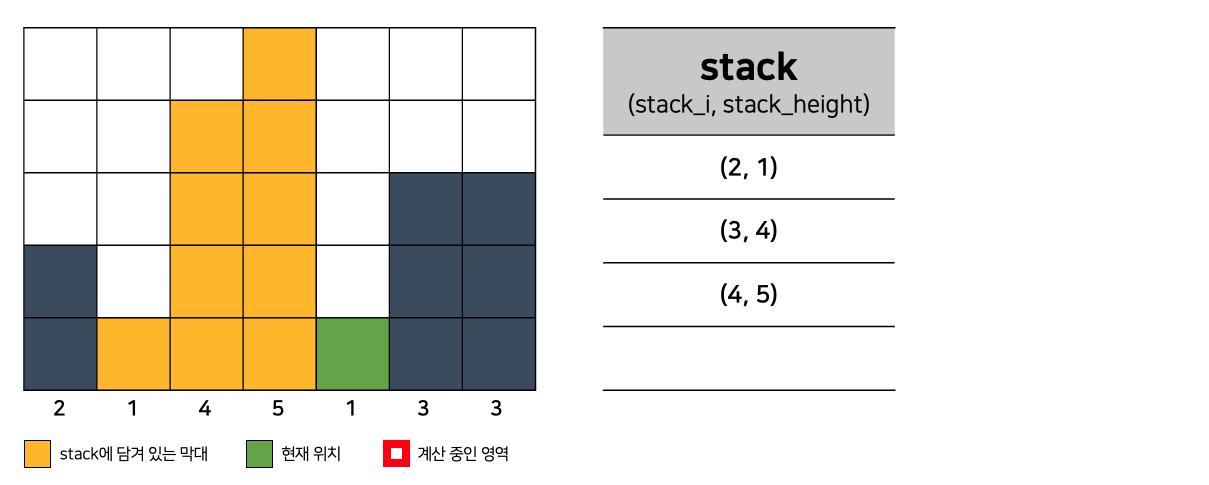
- stack에 2~4번째 막대가 들어있다.
- 현재 막대기는 길이가 1로, 직전 막대(4, 5)보다 길이가 짧아서 더이상 stack에 추가하지 않고,
2단계로 돌아가 stack에 들은 막대들의 넓이를 계산한다.
5. 스택에 마지막으로 들어간 막대 보다 짧은 막대를 만나면 스택에 들어있는 막대의 넓이를 계산한다. (2단계와 유사)
- 이 경우는 2단계에서 본 경우와 stack에 들어있는 값의 개수가 달라서 계산식이 조금 추가되어야 한다ㅜㅜ
(2단계에서는 stack에 값이 하나만 들어있었음) - 일단 스택에서 하나씩 pop하면서 최근에 넣은 것부터 꺼내서 넓이를 계산한다.
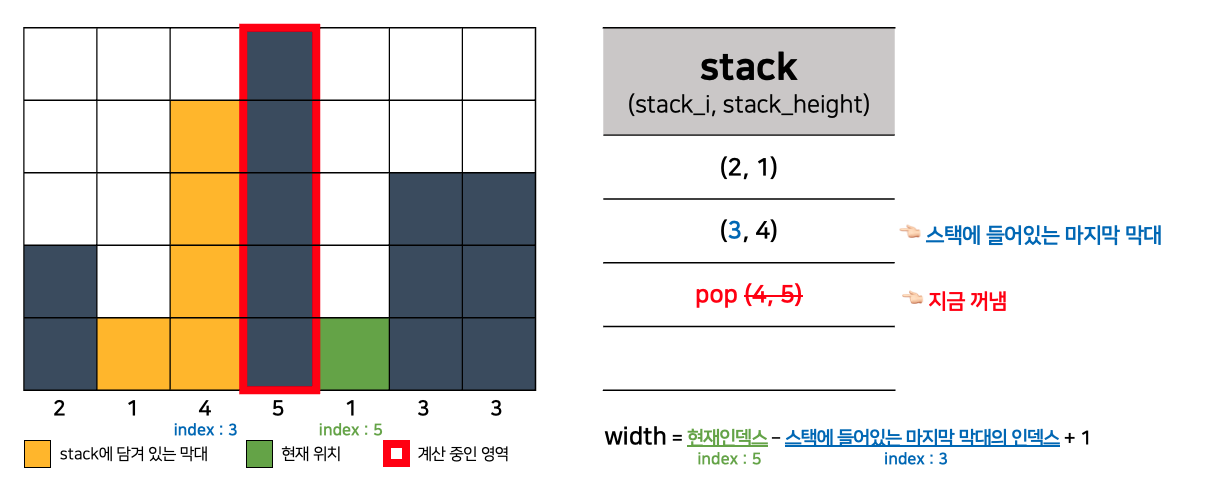
- 이때 width는 stack에 들어있는 마지막 인덱스에 1을 더한 것을 현재 인덱스에서 빼주면 된다.
width = 현재인덱스 - 스택의_마지막_막대_인덱스 + 1 - 👆 width를 이렇게 구해야 하는 이유는 바로 다음 예시에서 더 명확히 알 수 있다.
바로 하나 더 꺼내보자 ㄱㄱ
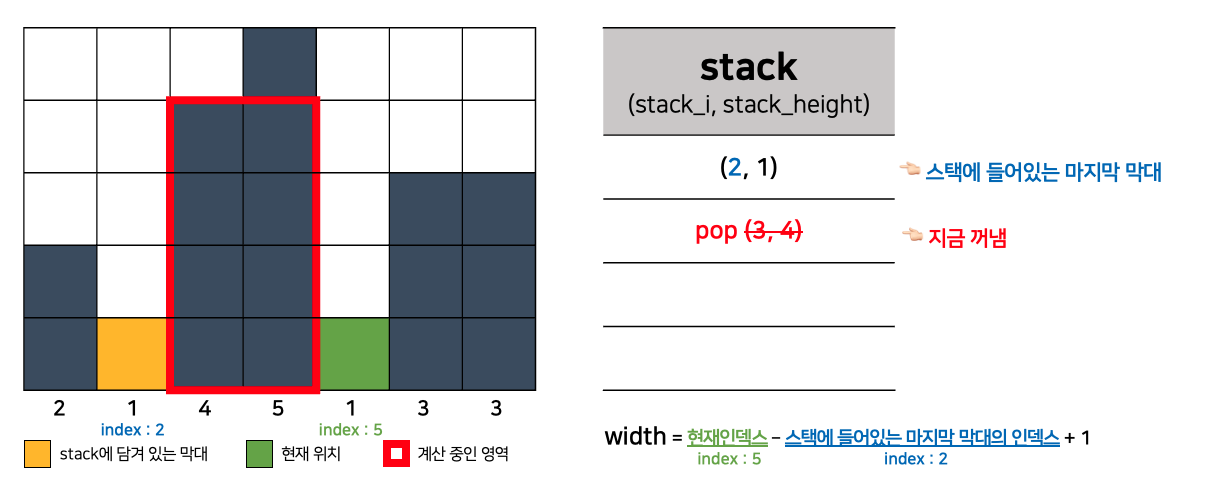
- 바로 이런 경우 때문에 width를
stack에 남아있는 마지막 막대의 index +1에서부터 계산해준 것이다! - stack에 들어있는 막대는 오름차순으로 들어오므로,
당연히 현재 위치로 오기 직전까지 만날 막대들은 stack에서 지금 꺼낸 막대보다 길이가 길거나 같을 것이다.
(짧은건 꺼내서 이미 계산하고 버렸으니 안 들어있음) - 따라서
현재 위치에서 이막대가 시작되는 위치까지를 너비로 계산해줘야 한다.
🤔 그렇다면, 그냥 꺼낸 막대의 인덱스로 계산해도 될 것 같은데?
이런 의문이 생긴다면 아래 예시를 보자
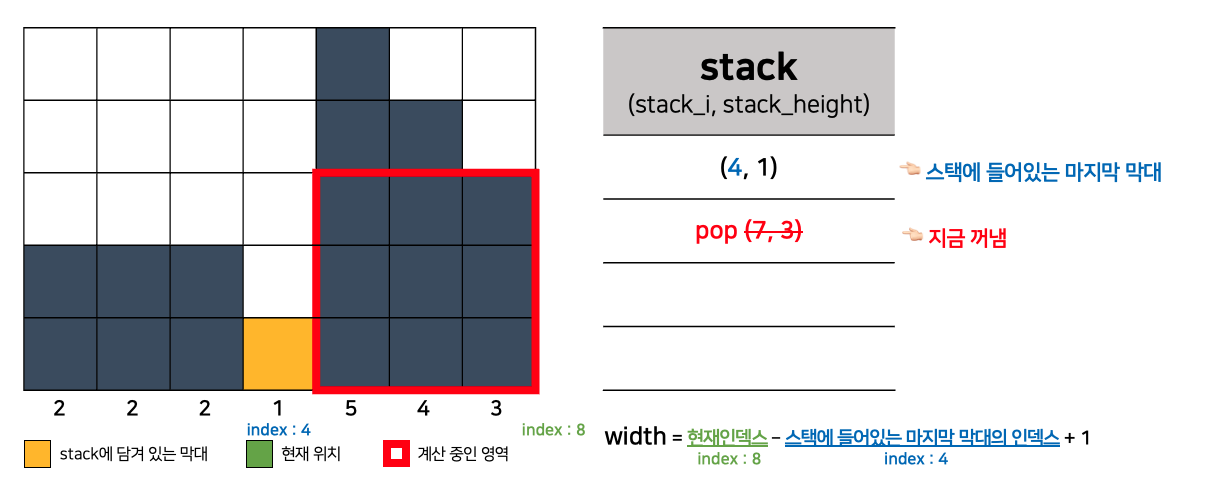
- 그래프가 내림차순으로 주어진 경우에는
6번째 반복부터는 스택에서 pop을 해가면서 막대를 꺼내 계산하고 버렸을 것이다. - 그렇게 되면 이 영역을 계산할 때는 이미 (6, 4), (5, 5)는 이전 계산에서 pop해서 사라졌으므로
width를 3으로 하는 저만큼의 영역을 계산할 수가 없다. - 따라서, 스택에 들어있는 마지막 막대의 인덱스 + 1 부터 현재 인덱스까지를 width로 잡아야 한다.
6. 반복이 종료된 후 스택에 남은 막대가 있는지 확인한다.
- stack에는 현재 막대보다 길거나 같은 것을 추가한다.
- 막대의 넓이를 계산하는 것은 stack에 들어있는 것보다 짧은 막대가 나오는 순간뿐이다.
- 그렇다면 계속해서 길이가 같거나 더 길어지게 주어진 경우에는 계산을 안하겠지?!?
- 위의 4단계에서 들었던 예시도 해당되고, 문제에서 두번째 예시로 주어진 입력도 해당된다.
문제에서 주어진 예시로 아라보쟈🌟
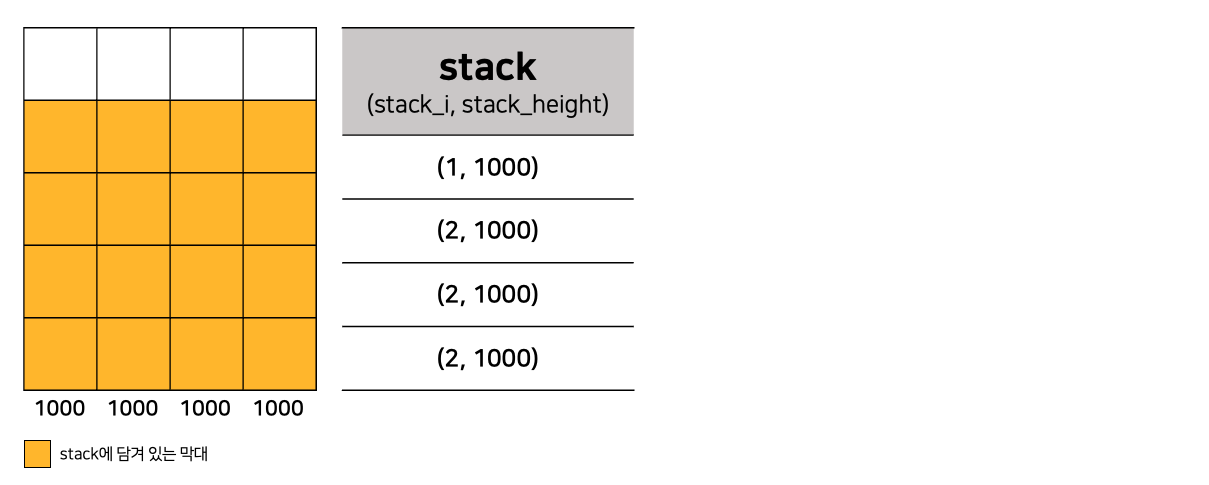
- 바로 이런 경우! stack에 담기만 하고 계산은 하지 않는다..🙄
- 따라서, 반복문이 종료되고 나서 stack에 값이 남아있다면 그 안에 남아있는 막대들의 넓이를 계산해줘야 한다.
# 반복이 종료되고, 스택에 남은 막대기가 있다면 계산합니다.
while stack:
stack_i, stack_height = stack.pop()
width_start = 1
if stack:
width_start = stack[-1][0]+1
result = (graph[0]+1 - width_start) * stack_height
max_result = max(result, max_result)- 방법은 유사하지만, width를 구하는 부분만 조금 다르다.
- 이 경우에는 이미 반복문의 끝까지 왔으므로 width의 끝지점이
i가 아니다.
막대의 개수 + 1에 해당하는graph[0]+1을 width의 끝지점으로 계산한다.width = graph[0]+1 - width_start
끝~
전체 코드
from sys import stdin
while True:
graph = list(map(int, stdin.readline().split()))
# 0이 입력되면 반복문을 종료합니다.
if graph[0] == 0:
break
# 스택과 최대 직사각형 넓이를 저장할 변수를 초기화합니다.
stack = []
max_result = 0
for i, height in enumerate(graph):
if i == 0: # 첫 번째 i는 막대기의 개수를 의미하므로 넘어갑니다.
continue
# 스택의 가장 위쪽 막대기보다 현재 막대기의 높이가 작으면
if stack and stack[-1][1] > height:
while stack: # 스택에서 빼내며 최대 직사각형 넓이를 계산합니다.
stack_i, stack_height = stack.pop()
width_start = 1
if stack:
width_start = stack[-1][0]+1
result = (i - width_start) * stack_height
max_result = max(result, max_result) # 최대값 갱신
# 스택에 들어있는 막대 중에서 현재 막대의 길이보다 큰 것들만 꺼내서 계산합니다.
if not stack or stack[-1][1] <= height:
break
# 스택이 비어 있거나 스택의 가장 위쪽 막대기보다 현재 막대기의 높이가 크거나 같으면
if not stack or stack[-1][1] <= height:
stack.append((i, height)) # 스택에 현재 막대기를 추가합니다.
# 반복이 종료되고, 스택에 남은 막대기가 있다면 계산합니다.
while stack:
stack_i, stack_height = stack.pop()
width_start = 1
if stack:
width_start = stack[-1][0]+1
result = (graph[0]+1 - width_start) * stack_height
max_result = max(result, max_result) # 최대값 갱신
# 최대 직사각형 넓이를 출력합니다.
print(max_result)728x90
반응형
'Algorithm' 카테고리의 다른 글
| [python] 백준 2261 :: 가장 가까운 두 점 (분할 정복) (0) | 2023.03.14 |
|---|---|
| [python] 백준 10000 :: 원 영역 (스택) (1) | 2023.03.14 |
| [python] 백준 13334 :: 철로 (우선순위 큐) (0) | 2023.03.13 |