[python] 백준 9020 :: 골드바흐의 추측 (소수 찾기, 소수 배열 짱 빨리 만들기)
2023. 3. 7. 16:34ㆍAlgorithm
728x90
반응형
소수 찾기: 배수 제거 방식
소수를 찾을 때 에라토스테네스의 체를 이용하는 방법보다
더 빠르게 찾을 수 있는 방법이 있다.
1부터 소수를 찾아나가면서, 배수를 지워버리는 방법이다.
숫자의 배수들은 소수가 아니므로, 소수인지 검증하기 위해 다른 숫자들로 나눠볼 필요가 없다!!
전체 코드
prime = [] # 소수를 담을 배열
check = [False]+[False] + [True] * 9999 # index에 해당하는 숫자가 소수일 때만 True를 담을 배열
# 2부터 10000까지 소수 찾기 시작~!
for number in range(2, 10001):
if check[number]:
# True가 담겨있으면 소수임! 👉🏻 prime 배열에 추가한다.
prime.append(number)
# 찾은 소수의 배수들을 check 배열에서 False로 바꿔준다.
# 👉🏻 False로 바뀐 것들은 위 코드에서 prime 배열에 추가되지 않는다.
for i in range(number*2, 10000, number):
check[i] = False1. 실제 소수를 담을 배열 prime과 소수인지 여부를 담을 배열 check를 각각 만든다.
prime = [] # 소수를 담을 배열
check = [False]+[False] + [True] * 9999 # index에 해당하는 숫자가 소수일 때만 True를 담을 배열prime: 이 배열에는 실제 소수를 담을 것이다.check: 이 배열의 Index가 소수라면 True를, 소수가 아니라면 False를 담을 것이다.
초기에는[False, False, True, True ..., True]를 담아둔다.
🤔 False를 두개 담아놓는 이유는? 👉🏻 0과 1은 소수가 아니니까~!
# check 배열에 담길 값들을 미리 보자! 👀
check[0] = False
check[1] = False
check[2] = True # 이렇게 소수일 경우에만 True로 그대로 두고, (2는 소수 ⭕️)
check[3] = True # (3은 소수 ⭕️)
check[4] = False # 소수가 아니면 아래 2단계에서 False로 바꿔줄 것이다. (4는 소수가 아님 ❌)
...
2. 소수 찾기 고고
2단계가 잘 이해되지 않는다면, 3단계 먼저 읽어보긔 😊
# 2부터 10000까지 소수 찾기 시작~!
# number가 소수인지 검증한다.
for number in range(2, 10001):
if check[number]:
# True가 담겨있으면 소수임! 👉🏻 prime 배열에 추가한다.
prime.append(number)
... # 3단계에서 이어짐반복문의 범위
range(2, 10001)- 10000보다 작거나 같은 수
number <= 10000중에서 소수에 해당하는 값을 찾을 것이다.
( 🤔왜 10000? 👉🏻 문제에 제시된 가장 큰 수가 10000임ㅋㅎ ) - 0과 1은 어차피 소수가 아니니까 2부터 10000까지 반복문을 돌려돌려🌪
소수인지 검증
if check[number]- 이 for문 안에서 조건문으로 number가 소수인지 검증한다.
check배열에 담긴 값이True라면, 해당 Index에 해당하는 숫자는 소수이다.
(3단계에서 그렇게 만들 거임)- 위에서
check[2]에True를 넣어놨는데,
2는 소수이므로 일단 소수인지 검증할 필요가 없다. (즉, number가 2일 때는 당연히 실행되는 조건문이다.)
소수라면 prime에 추가
prime.append(number)- 조건이
True라면 소수를 담는 배열인prime에number를 추가한다.
🔥 이제부터가 진짜 검증 시작임!!
3. number의 배수들을 check 배열에서 False로 바꿔준다.
아래 코드는 위의 2단계 코드에서 이어진다.
# 2부터 10000까지 소수 찾기 시작~!
# number가 소수인지 검증한다.
for number in range(2, 10001):
if check[number]:
# True가 담겨있으면 소수임! 👉🏻 prime 배열에 추가한다.
prime.append(number)
🚨🚨🚨 이 아래부터가 3단계 🚨🚨🚨
# 찾은 소수의 배수들을 check 배열에서 False로 바꿔준다.
# 👉🏻 False로 바뀐 것들은 위 코드에서 prime 배열에 추가되지 않는다.
for i in range(number*2, 10000, number):
check[i] = False배수 찾기
for i in range(number*2, 10000, number):- 지금 반복문에서 돌고있는 number 변수의 배수들은 소수가 아니다.
예를 들어, number가 2라면 4, 6, 8 ... 등 2의 배수들은 소수가 아님- 그러므로
check배열에서number의 배수들에 해당하는 index에False값을 넣어줄 것이다. - 반복문의 범위는
시작:number의 2배수
끝:마지막 숫자
간격:number
이렇게 하면 number의 2배수부터 마지막 숫자 전까지 number의 배수들이 하나씩i에 들어온다.
끝!@
이제 바깥 반복문에서는 여기서 False를 넣은 number인 경우 if문의 조건에 맞지 않아
다음 반복으로 넘어가게 된다.
속도 비교
다른 방법들과 속도를 비교해보았다.
다른 방법들에는 에라토스테네스의 체를 모두 적용했다.
비교 결과 스포
👉🏻 배수 제거 방식이 제일 빠름 😊
- 다른 방식들은 배수 제거 방식보다 무려
4.8배나 더 반복한다. - 속도도
4~5배!
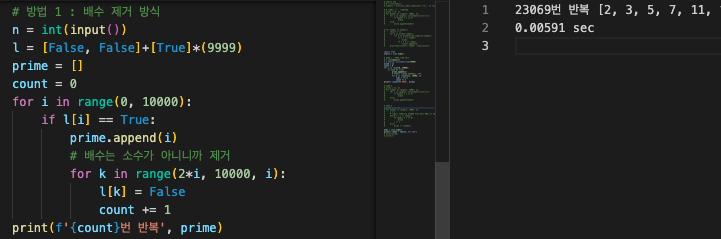
1. 위에서 설명한 배수 제거 방식
2. for문과 에라토스테네스의 체를 이용해서 number보다 작은 수로 나눠보는 방식

prime = [2, 3]
for number in range(5, 10001, 2):
for i in range(2, int(number**(1/2))+1):
if number % i == 0:
break
else:
prime.append(number)3. 2번과 동일하지만 while 사용

prime = [2, 3]
for number in range(5, 10001, 2):
i = 2
while i * i <= number:
if number % i == 0:
break
i += 1
else:
prime += [number]
[골드바흐의 추측]
# 문제
1보다 큰 자연수 중에서 1과 자기 자신을 제외한 약수가 없는 자연수를 소수라고 한다. 예를 들어, 5는 1과 5를 제외한 약수가 없기 때문에 소수이다. 하지만, 6은 6 = 2 × 3 이기 때문에 소수가 아니다.
골드바흐의 추측은 유명한 정수론의 미해결 문제로, 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다는 것이다. 이러한 수를 골드바흐 수라고 한다. 또, 짝수를 두 소수의 합으로 나타내는 표현을 그 수의 골드바흐 파티션이라고 한다. 예를 들면, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5, 12 = 5 + 7, 14 = 3 + 11, 14 = 7 + 7이다. 10000보다 작거나 같은 모든 짝수 n에 대한 골드바흐 파티션은 존재한다.
2보다 큰 짝수 n이 주어졌을 때, n의 골드바흐 파티션을 출력하는 프로그램을 작성하시오. 만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력한다.
# 입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고 짝수 n이 주어진다.
# 출력
각 테스트 케이스에 대해서 주어진 n의 골드바흐 파티션을 출력한다. 출력하는 소수는 작은 것부터 먼저 출력하며, 공백으로 구분한다.1. 소수를 찾는다.
import sys
N = int(input())
numbers = [int(sys.stdin.readline()) for _ in range(N)]
prime = [] # 소수를 담을 배열
check = [False]+[False] + [True] * 9999 # index에 해당하는 숫자가 소수일 때만 True를 담을 배열
# 2부터 10000까지 소수 찾기 시작~!
for number in range(2, 10001):
if check[number]:
# True가 담겨있으면 소수임! 👉🏻 prime 배열에 추가한다.
prime.append(number)
# 찾은 소수의 배수들을 check 배열에서 False로 바꿔준다.
# 👉🏻 False로 바뀐 것들은 위 코드에서 prime 배열에 추가되지 않는다.
for i in range(number*2, 10000, number):
check[i] = False- 소수를 찾아서 prime 배열에 넣어놓는다.
- n은 최대 10,000까지 주어지므로, 10000까지만 구해주면 된다.
2. 합이 number가 되는 소수의 쌍을 찾는다.
for number in numbers:
result = []
# 소수를 하나씩 변수 p로 가져온다.
for p in prime:
# 대소가 반전되고 나오는 건 똑같은 쌍이니까 👉🏻 또 따질 필요 없어서 break!
if p > number - p:
break
# (number - p)가 소수이면 => 소수의 합으로 number를 나타낼 수 있음
if check[number - p]:
result.append(p)
합이 number가 되는 소수들의 조건
- 일단,
prime배열로 반복문을 돌려서 소수를 하나씩 가져온다.p변수에 소수가 하나씩 담긴다. - 가져온 소수
p와 다른 소수의 합이number가 되는 경우를 찾아야 한다. number - p가 소수라면p와number - p가 합이number가 되는 소수의 쌍이다.
조건에 맞는 p 찾기
if p > number - p:
break- (
p,number - p) 쌍 중에서
(3, 5) 쌍과 (5, 3) 쌍은 동일한 쌍이므로 중복으로 따질 필요가 없다. - 따라서,
number - p가p보다 작아지면 반복문을 종료한다.
if check[number - p]:
result.append(p)p는 prime 배열에서 하나씩 꺼내온 거니까 당연히 소수이고,number - p가 소수인지 확인해야 한다.- 소수를 찾을 때 만든 배열 check에서 소수인지 검증할 숫자 인덱스가
True이면 소수인 것을 이용한다. - 소수라면, 합이 number가 되는 소수 쌍을 찾았으므로,
p를 result 배열에 넣어둔다.
(p의 짝은number - p로 구하면 되니까 p만 저장 ㄱ ㄱ)
3. 두 소수의 차이가 가장 작은 것 구하기
# 가능한 p 중에서 제일 큰 p 찾기
print(max(result), number-max(result))- 소수의 쌍은 위에서 구한
p와number - p이다. - 즉, 두 소수의 차이가 가장 작은 쌍은
p가 가장 큰 경우를 찾으면 된다. - result 배열의 최대값을 찾고, 대응되는 짝을 구해 출력한다.
끝~
골드바흐의 추측 전체 코드
import sys
N = int(input())
numbers = [int(sys.stdin.readline()) for _ in range(N)]
prime = [] # 소수를 담을 배열
check = [False]+[False] + [True] * 9999 # index에 해당하는 숫자가 소수일 때만 True를 담을 배열
# 2부터 10000까지 소수 찾기 시작~!
for number in range(2, 10001):
if check[number]:
# True가 담겨있으면 소수임! 👉🏻 prime 배열에 추가한다.
prime.append(number)
# 찾은 소수의 배수들을 check 배열에서 False로 바꿔준다.
# 👉🏻 False로 바뀐 것들은 위 코드에서 prime 배열에 추가되지 않는다.
for i in range(number*2, 10000, number):
check[i] = False
# 소수의 합 쌍 찾기 시작~!
for number in numbers:
result = []
# 소수를 하나씩 가져온다.
for p in prime:
# 대소가 반전되고 나오는 건 똑같은 쌍이니까 👉🏻 또 따질 필요 없어서 break!
if p > number - p:
break
# (number - p)가 소수이면 => 소수의 합으로 number를 나타낼 수 있음
if check[number - p]:
result.append(p)
# 가능한 p 중에서 제일 큰 p 찾기
print(max(result), number-max(result))728x90
반응형
'Algorithm' 카테고리의 다른 글
| [python] 백준 2628 :: 종이자르기 (0) | 2023.03.07 |
|---|---|
| [python] 백준 1065 :: 한수 (숫자의 각 자릿수 구하기) (0) | 2023.03.07 |
| [JavaScript] 프로그래머스 :: 최소직사각형 (0) | 2022.12.10 |