[python] 백준 9663 :: N-Queen 👑
2023. 3. 7. 21:18ㆍAlgorithm
728x90
반응형
[N-Queen]
# 문제
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.
N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
# 입력
첫째 줄에 N이 주어진다. (1 ≤ N < 15)
# 출력
첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.풀이
전체 코드
N = int(input())
# row[행_idx] == True면 퀸이 있는 행
row = [False] * N
# 열_idx + 행_idx == True면 퀸이 있음
right_cross = [False] * (2 * N - 1)
# 열_idx - 행_idx + N-1 == True면 퀸이 있음
left_cross = [False] * (2 * N - 1)
# 퀸의 조합 개수
count = 0
def recursive(col_idx):
global count
# 열 인덱스가 N이면 퀸을 모두 놓은 거니까 count++ 해주고 리턴
if col_idx == N:
count += 1
return
for row_idx in range(N):
# row_idx 행에 퀸이 없고
if (not row[row_idx]
# 왼쪽 대각선에도 퀸이 없고
and not left_cross[N-1 + col_idx - row_idx]
# 오른쪽 대각선에도 퀸이 없으면
and not right_cross[col_idx + row_idx]):
# row_idx 행에 퀸을 놓는다.
row[row_idx] = True
left_cross[N-1 + col_idx - row_idx] = True
right_cross[col_idx + row_idx] = True
# 다음 열에 놓을 퀸 찾으러 ㄱㄱ
recursive(col_idx + 1)
# 다음 반복에서는 이 행에 놓는 경우가 아니니까 False로 바꿔둔다.
row[row_idx] = False
left_cross[N-1 + col_idx - row_idx] = False
right_cross[col_idx + row_idx] = False
recursive(0)
print(count)0. 풀이 방법
- 퀸은 모든 행, 열, 양쪽 대각선에서 홀로 위치해야 한다.
(스도쿠랑 비슷?!🙂) - 인자로 열의 index를 0부터 차례대로 받고, 몇번째 행 index에 들어갈 수 있는지 찾는 함수를 만든다.
- 반복문을 통해 0부터 N-1까지 행 중에서
1) 퀸이 놓이지 않은 행인지2) 오른쪽 위 대각선 방향으로 퀸이 놓이지 않았는지3) 왼쪽 위 대각선 방향으로 퀸이 놓이지 않았는지
위 세가지를 확인해서 퀸이 놓이지 않은 경우에 퀸을 배치한다.
1. 중복을 체크할 배열을 만든다.
각 배열에서
값이 True이면 퀸이 이미 있는 것이고,False인 경우에는 퀸이 없어서 배치할 수 있는 것이다.
1) 행 중복 체크 배열
row = [False] * Nrow[행_idx] == True면 퀸이 있음- 배열의 길이는 N
2) 오른쪽 위 방향 대각선 중복 체크 배열
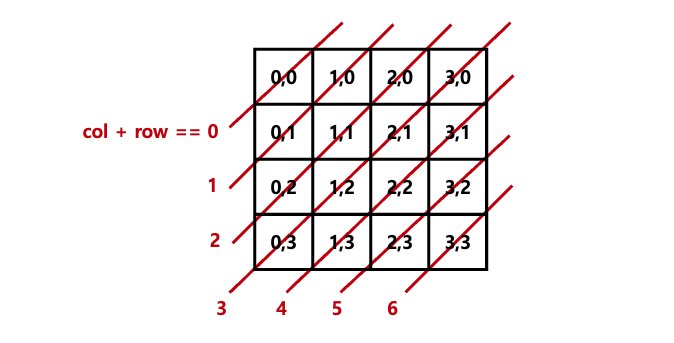
right_cross = [False] * (2 * N - 1)right_cross[열_idx + 행_idx] == True면 퀸이 있음- 배열의 길이는 2N - 1
- 오른쪽 위를 향하는 대각선 배열 인덱스 정하기
👉🏻 열 index와 행 index를 더한 값으로 정한다.
3) 왼쪽 위 방향 대각선 중복 체크 배열
left_cross = [False] * (2 * N - 1)left_cross[열_idx - 행_idx + N-1] == True면 퀸이 있음- 배열의 길이는 2N - 1
- 왼쪽 위를 향하는 대각선 배열 인덱스 정하기
👉🏻 열 Index에서 행 index를 빼고, N-1을 더한 값으로 정한다.

2. 퀸을 모두 배치한 경우를 먼저 분기한다.
def recursive(col_idx):
global count
# 열 인덱스가 N이면 퀸을 모두 놓은 거니까 count++ 해주고 리턴
if col_idx == N:
count += 1
return- 함수의 인자로 열 index를 보내줄 거니까,
받은 인자의 값이 N과 같으면 모두 고른 것이다. - 모두 골랐으면, 문제에서 시키는 대로 결과로 출력할 개수
count에 +1을 해주고, 함수를 종료한다.
3. 퀸을 놓을 수 있는 곳을 찾는다.
for row_idx in range(N):
# row_idx 행에 퀸이 없고
if (not row[row_idx]
# 왼쪽 대각선에도 퀸이 없고
and not left_cross[N-1 + col_idx - row_idx]
# 오른쪽 대각선에도 퀸이 없으면
and not right_cross[col_idx + row_idx]):- 반복문을 통해 나오는 0부터 N-1까지의 값이 행 (
row_idx)이 된다. - 함수의 인자로 받는 값(
col_idx)가 열이다.
_이름 그대로..😅 _ - 열은 중복을 체크할 필요가 없다! 이 열에는 지금 퀸을 배치하는 순간이 처음 놓아지는 것이다.
- 해당
row_idx행에 퀸이 배치되어있지 않은지 확인한다. - 왼쪽 대각선과 오른쪽 대각선에도 마찬가지로
퀸이 배치되어있지 않은지 확인한다. - 세 배열에서 찾은 값이 모두
False라면, 퀸을 놓을 자리를 찾은 것이다!! 🔥
4. 찾은 자리에 퀸을 놓았다는 것을 표시해둔다.
# col_idx 열 & row_idx 행에 퀸을 놓는다.
row[row_idx] = True
left_cross[N-1 + col_idx - row_idx] = True
right_cross[col_idx + row_idx] = True- 다음 열에는 이 위치에 퀸을 놓으면 안되니까 True로 표시를 해둔다.
- 이러면 다음 열에서 퀸 위치를 찾을 때는 3단계의 조건문에 의해 이 위치에 퀸을 놓지 않겠지!!
5. 다음 열에서도 퀸을 놓을 자리를 찾으러 ㄱㄱ
# 다음 열에 놓을 퀸 찾으러 ㄱㄱ
recursive(col_idx + 1)col_idx가N과 같아질 때까지 3~5단계를 반복한다.col_idx가N과 같아지면, 2단계의 if문으로 빠지고 함수가 종료된다.
6. 다음 반복을 위해 중복 체크 배열을 되돌린다.
# 다음 반복에서는 이 행에 놓는 경우가 아니니까 False로 바꿔둔다.
row[row_idx] = False
left_cross[N-1 + col_idx - row_idx] = False
right_cross[col_idx + row_idx] = False- 여기서 의미하는 다음 반복은 recursive 함수의 반복이 아닌,
for문의 반복을 의미한다. - 즉, 지금 col_idx의 다른 행에 퀸을 배치하는 경우를 찾기 위해 for문이 돌아가는 거니까
지금 놓은 행의 위치는 없애줘야 한다. - 그러니까 원상복귀 ㄱㄱ 👉🏻 True로 바꾼 값을 다시 False 값으로 바꿔준다.
👑끝👑
728x90
반응형
'Algorithm' 카테고리의 다른 글
| [python] 백준 1074 :: Z (0) | 2023.03.07 |
|---|---|
| [python] 백준 5568 :: 카드 놓기 (재귀 함수 vs itertools 비교) (0) | 2023.03.07 |
| [python] 백준 2628 :: 종이자르기 (0) | 2023.03.07 |